Simulación y probabilidades para Clasificatorias Sudamericanas 2018
¿Recuerdan esos tiempos en que todo Chile (incluído nuestro técnico) sacaba la calculadora para ver cuántos puntos necesitábamos para clasificar?
Nadie echa de menos esos tiempos, pero yo decidí llevar esto al límite y, de paso, sacarme un par de dudas acerca de simulaciones de torneos.
El objetivo de este post es mostrar cómo se puede formular algo probabilísticamente y cómo podemos simular (y luego graficar!) para responder nuestras preguntas.
La gran pregunta será: ¿Cuál es la probabilidad de Chile salga al menos quinto en las clasificatorias?
Nota
Estas simulaciones fueron corridas justo antes de que jugase la 16ava fecha. Si hay interés, puedo volver a correr los gráficos y ver cómo cambiaron las distribuciones
Aproximación
Puesto que hablamos de probabilidad, necesitamos definir qué es el espacio muestral en este contexto. El espacio muestral es el conjunto de todos los posibles resultados de un suceso aleatorio. Por ejemplo, lanzar un dado tiene 6 posibles resultados: $1, 2, 3, 4, 5$ y $6$. Si lanzo dos dados, hay 36 posibles resultados: $(1, 1), (1, 2), …, (1, 6), (2, 1), …, (2, 6), …, (6, 1), …, (6, 6) $
Para las Clasificatorias, un resultado (o mundo posible) será la combinación de resultados de TODOS los partidos que serán disputados de aquí hasta el final de las clasificatorias. Por ejemplo, en un mundo posible Brasil le gana a Colombia en la fecha 15 y Argentina pierde con Uruguay. En otros mundo posible los dos partidos terminan en empate. El resultado final de esta combinación de partidos será una table de puntaje.
Por ejemplo, $\omega_1$ (un resultado o mundo posible) podría tener esta tabla
| Equipo | puntos |
|---|---|
| Brasil | 36 |
| Colombia | 25 |
| Uruguay | 28 |
| Chile | 31 |
| Argentina | 28 |
| Ecuador | 25 |
| Perú | 24 |
| Paraguay | 22 |
| Bolivia | 16 |
| Venezuela | 14 |
mientras que $\omega_2$ podría tener:
| Equipo | puntos |
|---|---|
| Brasil | 37 |
| Colombia | 36 |
| Uruguay | 28 |
| Chile | 25 |
| Argentina | 24 |
| Ecuador | 28 |
| Perú | 22 |
| Paraguay | 20 |
| Bolivia | 20 |
| Venezuela | 9 |
El número de $\omega$ es finito en nuestro caso, lo que debiera facilitar las cosas.. Para obtener la probabilidad de que Chile salga cuarto, podríamos tomar un camino que parece sencillo:
- definir una probabilidad para cada uno de estos $\omega$. y luego:
- sumar las probabilidades de los $\omega$ donde Chile sale al menos cuarto
Lamentablemente hay dos problemas
- Hay demasiados $\omega$! Cada fecha tiene 5 partidos, con tres posibles resultados, lo que da $3^5 = 243$ resultados por fecha. Si no me fallan mis habilidades combinatorias, puesto que tenemos $4$ fechas restantes, el total de combinaciones posibles es $243^4 = 3486784401$
- No es claro cómo asignar probabilidades a cada uno de esos $\omega$
Para solucionar el problema de manera simple, voy a hacer algunos supuestos.
Primero, voy a asumir que cada partido es independiente. Esto es, la probabilidad de que, por ejemplo, Uruguay le gane a Brasil de local es 30% y esta probabilidad no cambia si en el partido anterior Venezuela perdió contra Colombia o no. Esto no es realista, pero nos permite avanzar y no es claro que haya un sesgo hacia alguna dirección; en otras palabras, no me parece que asumir independencia introduzca un sesgo claramente positivo (o claramente negativo) a la estimación de la probabilidad de Chile salga al menos cuarto.
Segundo, para solucionar el problema de la gran cantidad de estados posibles, voy a simular para obtener draws de la distribución final. Asumiré las probabilidades para cada partido y con eso simularé todos los partidos de la fecha, luego todas las fechas para obtener uno de esos $\omega$ explicados arriba. La probabilidad de un $\omega$ estará dado por qué tan frecuentemente aparece en la simulación.
Esto puede sonar un poco curioso, pero es un ejemplo de método de Montecarlo
Para partir, importaré un par de paquetes de python y luego define el índice de cada equipo para trabajar después con matrices.
También escribo los encuentros para cada fecha.
%matplotlib inline
import numpy as np
import pandas as pd
import seaborn as sns
equipos = {'Brasil': 0, 'Colombia': 1, 'Uruguay': 2, 'Chile': 3, 'Argentina': 4, 'Ecuador': 5,
'Perú': 6, 'Paraguay': 7, 'Bolivia': 8, 'Venezuela': 9}
puntos_inicio = [33, 24, 23, 23, 22, 20, 18, 18, 10, 6]
equipos_a_puntos = {}
ind_a_puntos = {}
for eq, puntos in zip(equipos.keys(), puntos_inicio):
equipos_a_puntos[eq] = puntos
ind_a_puntos[equipos[eq]] = puntos
def fecha_to_indices(datos_fecha):
indices = np.empty((5, 2), dtype=int)
for i, fecha in enumerate(datos_fecha):
indices[i] = [equipos[fecha[0]], equipos[fecha[1]] ]
return indices
fecha15 = [['Chile', 'Paraguay'], ['Brasil', 'Ecuador'],
['Venezuela', 'Colombia'], ['Perú', 'Bolivia'], ['Uruguay', 'Argentina']]
fecha15Ind = fecha_to_indices(fecha15)
fecha16 = [['Colombia', 'Brasil'], ['Paraguay', 'Uruguay'],
['Argentina', 'Venezuela'], ['Ecuador', 'Perú'],
['Bolivia', 'Chile']]
fecha16Ind = fecha_to_indices(fecha16)
fecha17 = [['Colombia', 'Paraguay'], ['Chile', 'Ecuador'],
['Argentina', 'Perú'], ['Venezuela', 'Uruguay'],
['Bolivia', 'Brasil']]
fecha17Ind = fecha_to_indices(fecha17)
fecha18 = [['Paraguay', 'Venezuela'], ['Brasil', 'Chile'],
['Ecuador', 'Argentina'], ['Perú', 'Colombia'],
['Uruguay', 'Bolivia']]
fecha18Ind = fecha_to_indices(fecha18)
result_to_scores = {'w': [3, 0], 'd': [1, 1], 'l': [0, 3]}
Ahora debemos tomar una decisión respecto de las probabilidades de ganar, perder o empatar de cada equipo.
Para simplificar las cosas, asumo que hay un 33% de probabilidad de ganar, perder o empatar para cada equipo. Nuevamente, esto no necesariamente introduce un sesgo, pero sería interesante ver qué pasa cuando se ponene probabilidades más razonables.
Para facilitar hacer cualquier cambio, escribí la función mod_matriz_prob
La matriz de probabilidades de ganar o empatar queda en matriz_prob
fecha_to_prob es una función auxiliar para elegir solamente las probabilidades relevantes para la fecha. Por ejemplo, si Brasil juega contra Colombia, no me interesa la probabilidad de Brasil contra Uruguay.
### Matriz de probabilidades
# Filas son equipo local, columnas son equipo visita
# [0, 0] es Brasil contra Brasil, [0, 1] es Brasil de local contra Colombia de visita
# Cada posición tiene una entrada [p_ganar_local, p_empate]
# Inicializa con prior 1/3, 1/3
n_equipos = len(equipos)
matriz_prob = np.tile([1/3, 1/3], (n_equipos, n_equipos, 1))
def mod_matriz_prob(local, visita, nueva_prob, matriz_prob=matriz_prob):
"""
usa strings para modificar in-place el prior de [1/3, 1/3]
"""
matriz_prob[equipos[local], equipos[visita]] = nueva_prob
# Un ejemplo de modificación
# Brasil-Colombia (Brasil como local) tiene 50% de probabilidades
# de ganar, 30% de empatar (20% de perder)
# Colombia-Brasil (Colombia como local) tiene 30% de probabilidades de ganar
# 50% de empatar (20% de perder)
mod_matriz_prob('Brasil', 'Colombia', [0.5, 0.3])
mod_matriz_prob('Colombia', 'Brasil', [0.3, 0.5])
def fecha_to_prob(datos_fecha, matriz_prob=matriz_prob):
"""
Returns [ [prob_local_win, prob_draw] para cada juego en la fecha]
"""
probs = np.empty((5, 3))
for row, partido in enumerate(datos_fecha):
win_and_draw = matriz_prob[equipos[partido[0]], equipos[partido[1]]]
probs[row, :] = [win_and_draw[0], win_and_draw[1], 1 - win_and_draw[1] - win_and_draw[0]]
return probs
Ahora que hemos definido el comportamiento básico y algunas funciones auxiliares, necesitamos escribir las funciones que ejecuten la simulación propiamente tal.
Primero, una_fecha simula UNA realización de UNA fecha
Segundo, get_one_outcome usa una_fecha para obtener un outcome o resultado final (esto es, un ranking con los puntajes de los equipos).
Finalmente, simulate_k_outcomes repite get_one_outcome múltiples veces para tener una matriz con los resultados de la simulación.
def una_fecha(probfecha, fechaInd):
"""
Takes info of games in one date and get one realization.
Returns a vector of points to add. Each index associated to a country
"""
# iterate over each of 5 games
add_points = np.empty(n_equipos, dtype=int)
for i, game in enumerate(fechaInd):
game_outcome = np.random.choice(['w', 'd', 'l'], size=1, p=probfecha[i])[0]
add_points[[game[0], game[1]]] = result_to_scores[game_outcome]
return add_points
def get_one_outcome(probs_fechas, fechasInd, starting_scores, matriz_prob=matriz_prob):
"""
Returns a vector of points. Each index associated to a country
"""
# go over all fechas
ending_scores = np.zeros_like(starting_scores)
ending_scores += starting_scores
for j, probfecha in enumerate(probs_fechas):
ending_scores += una_fecha(probfecha, fechasInd[j])
return ending_scores
def simulate_k_outcomes(probs_fechas, fechasInd, starting_scores, matriz_prob=matriz_prob, reps=1000):
many_outcomes = np.empty((reps, n_equipos), dtype=int)
for rep in range(reps):
end_score = get_one_outcome(probs_fechas, fechasInd, starting_scores, matriz_prob)
many_outcomes[rep] = end_score
return many_outcomes
Voy a correr la simulación con $30000$ repeticiones, que debiera ser suficiente para obtener una buena idea de la distribución de resultados. Si estuviese haciendo esto más en serio, probaría con diferentes números para asegurarme que los resultados no cambien mucho.
El código no está para nada optimizado, así que estas 30 mil repeticiones toman unos 50 segundos en mi laptop.
Para hacer el trabajo más fácil, convierto esta matriz en un pd.DataFrame.
De aquí en adelante trabajaremos con este df. Cada una de las filas representa un mundo posible o realización de esta distribución de resultados finales.
# Corre/simula para k repeticiones
reps = 30000
probs_fechas = list(map(lambda x: fecha_to_prob(x, matriz_prob), [fecha15, fecha16, fecha17, fecha18]))
fechasInd = [fecha15Ind, fecha16Ind, fecha17Ind, fecha18Ind]
resultados_simul = simulate_k_outcomes(probs_fechas, fechasInd, puntos_inicio, reps=reps)
df = pd.DataFrame(resultados_simul)
df.columns = ['Brasil', 'Colombia', 'Uruguay', 'Chile', 'Argentina', 'Ecuador',
'Perú', 'Paraguay', 'Bolivia', 'Venezuela']
df.head(3)
| Brasil | Colombia | Uruguay | Chile | Argentina | Ecuador | Perú | Paraguay | Bolivia | Venezuela | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 41 | 30 | 25 | 27 | 26 | 24 | 24 | 23 | 15 | 14 |
| 1 | 35 | 32 | 26 | 30 | 27 | 27 | 20 | 27 | 15 | 11 |
| 2 | 42 | 28 | 27 | 26 | 27 | 28 | 21 | 20 | 15 | 15 |
Con este df se vuelve fácil responder preguntas. Por ejemplo, ¿cuál es la probabilidad de que Brasil salga primero? ¿Cuál es la probabilidad de que Ecuador tenga más puntos que Argentina?
Acá voy a responder la pregunta de la probabilidad de que Chile salga al menos cuarto y al menos quinto.
Los rankings pueden ser un problema. ¿Qué hago si Chile está empatado con Uruguay en el cuarto lugar? Si soy optimista, les asigno a los dos el cuarto lugar. Si soy pesimista, les asigno el quinto a ambos. Opté por darles a ambos el ranking 4.5, puesto que la simulación no tiene la diferencia de goles.
Obtenemos el ranking de Chile por fila, la frecuencia de esos rankings y luego hacemos un gráfico de barras de las frecuencias:
# Rank de Chile por fila.
df['rank_chile'] = df.rank(axis=1, ascending=False, ).iloc[:, 3]
df['frec'] = df.rank_chile.map(
(df.rank_chile.value_counts() /len(df) ).to_dict())
sns.barplot('rank_chile', 'frec', data=df)
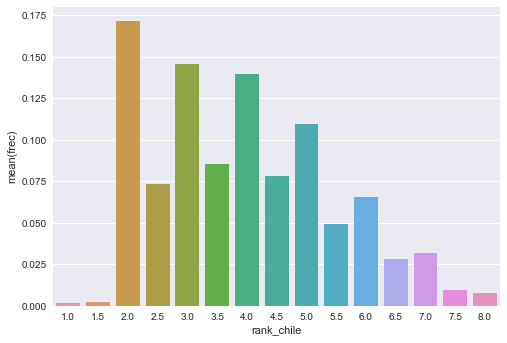
Ok! Hay buenas posibilidades de salir segundo, tercero y cuarto, pero también hay una cola de sexto y séptimo lugar.
Los 2.5 y 3.5 son más pequeños porque es un poco menos probables lograr empatas, que son los que generan estos rankings .5
Ahora veamos las probabilidades de salir entre los primeros 3, 4, 4.5 y 5
d = {}
d['mejores_4'] = len(df[df.rank_chile <= 4]) / len(df)
d['mejores_4_5'] = len(df[df.rank_chile <= 4.501]) / len(df)
d['mejores_5'] = len(df[df.rank_chile <= 5]) / len(df)
d['mejores_3'] = len(df[df.rank_chile <= 3]) / len(df)
pd.Series(d).to_frame(name="prob")
| prob | |
|---|---|
| mejores_3 | 0.395100 |
| mejores_4 | 0.619900 |
| mejores_4_5 | 0.698300 |
| mejores_5 | 0.807733 |
Bonus: distribuciones acumuladas
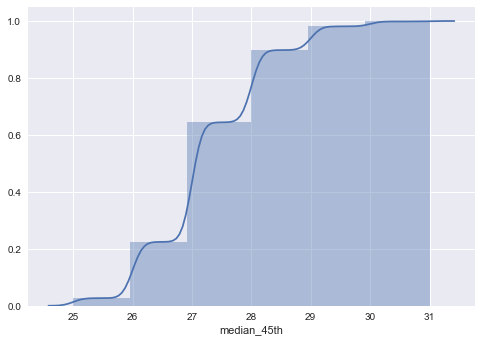
Como bonus, muestro la distribución acumuladas del puntaje mediano que tiene el lugar 4.5 en las distribuciones. Esto es una manera de ver qué puntaje es necesario tener para alcanzar al menos el lugar 4.5.
Se puede ver que 29 o 30 puntos parecen ser suficientes.
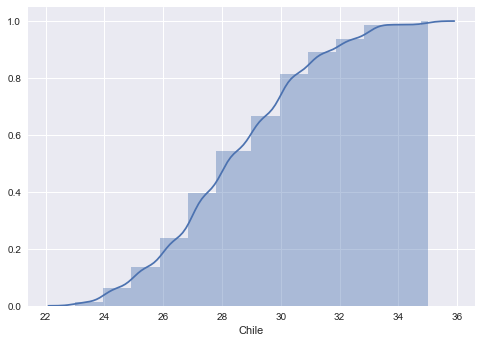
Abajo también hice un gráfico de la distribución acumulada de los puntos de Chile
df['median_45th'] = df[df.rank(axis=1, ascending=False, ) == 4.5].median(axis=1)
sns.distplot(df.median_45th[pd.notnull(df.median_45th)],
hist_kws=dict(cumulative=True),
kde_kws=dict(cumulative=True))
sns.distplot(df.Chile,
hist_kws=dict(cumulative=True),
kde_kws=dict(cumulative=True))